© 2025 Astra.si. Tutti i diritti riservati
"Per la prossima generazione."
© 2025 Astra.si. Tutti i diritti riservati
"Per la prossima generazione."
Nell'analisi matematica, uno dei concetti chiave è quello che descrive il cambiamento di una funzione rispetto al cambiamento del suo argomento. Questo concetto porta alla definizione formale della derivata, che è il fondamento per molte ulteriori costruzioni e teorie matematiche. L'idea centrale è che la derivata misura il tasso di variazione di una funzione in un dato punto – cioè, quanto rapidamente e in quale direzione la funzione sta cambiando lì.
Sia 'f' una qualsiasi funzione reale e x₀ un punto nel suo dominio. La derivata della funzione 'f' nel punto x₀ è denotata come f'(x₀) ed è definita come il limite del rapporto incrementale, se questo limite esiste:
f'(x₀) = lim (quando h → 0) [f(x₀ + h) - f(x₀)] / h.
In questa espressione, 'h' rappresenta una piccola variazione nella variabile indipendente x, mentre il numeratore mostra la variazione nel valore della funzione. Se questo limite esiste, diciamo che la funzione è differenziabile in quel punto.
Geometricamente, la derivata rappresenta la pendenza della retta tangente al grafico della funzione nel punto x₀. Se immaginiamo il grafico della funzione come una curva liscia, allora la tangente in un dato punto indica la direzione in cui la curva si sta dirigendo. Più grande è la derivata, più ripida è questa pendenza.
Usiamo la definizione:
f'(x) = lim (quando h → 0) [(x + h)^2 - x^2] / h = lim (quando h → 0) [x^2 + 2xh + h^2 - x^2] / h = lim (quando h → 0) [2xh + h^2] / h = lim (quando h → 0) (2x + h) = 2x.
Pertanto, la derivata della funzione x^2 è 2x. Questo significa che i valori di questa funzione nel punto x stanno cambiando a un tasso di 2x.
La derivata è uno strumento matematico per descrivere il tasso di variazione di una funzione. Usando il limite del rapporto incrementale, arriviamo a una definizione precisa che ha sia un significato numerico che geometrico. Comprendendo esempi di base, come la funzione quadratica, possiamo costruire più facilmente la conoscenza su funzioni più complesse.
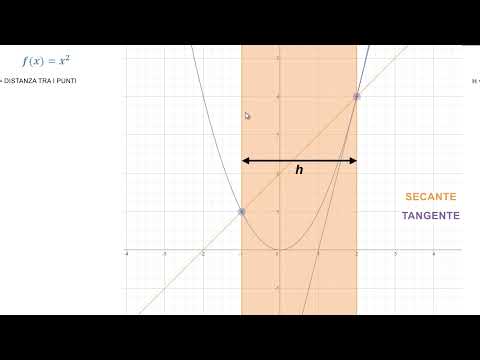
Cos'è una Derivata?
Spiegazione
13 minuti
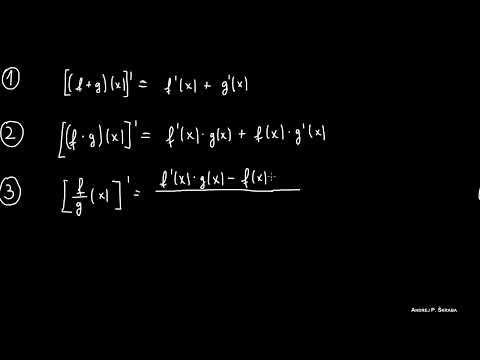
Regole di Derivazione
Spiegazione
4 minuti
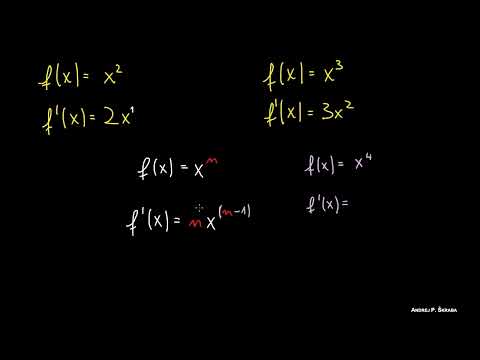
Regole per Calcolare la Derivata di una Funzione
Spiegazione
5 minuti

Derivata per Definizione 1
Spiegazione
6 minuti
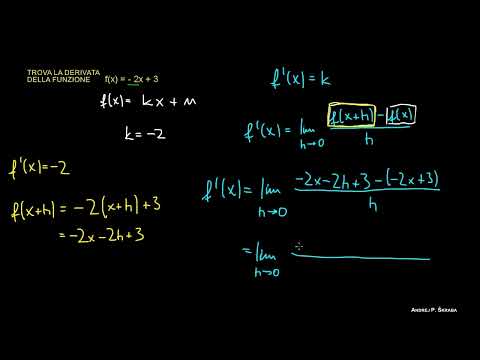
Derivata per Definizione 2
Spiegazione
5 minuti

Derivata – Esercizio 1
Spiegazione
6 minuti
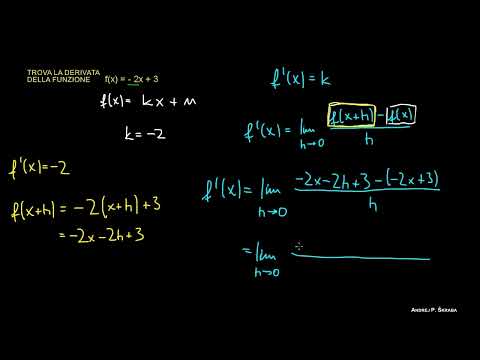
Derivata – Esercizio 2
Spiegazione
5 minuti

Derivata – Esercizio 3
Spiegazione
4 minuti